
Properties of Ductile Cast Iron – ASTM A536 – 60-40-18. Ductile iron is stronger and more shock resistant than gray iron. Ductile iron has mechanical characteristics approaching those of steel, while it retains high fluidity when molten and lower melting point.
Ductile iron, also known as nodular iron or spheroidal graphite iron, is very similar to gray iron in composition, but during solidification the graphite nucleates as spherical particles (nodules) in ductile iron, rather than as flakes. Ductile iron is not a single material but part of a group of materials which can be produced with a wide range of properties through control of their microstructure. The matrix phase surrounding these particles is either pearlite or ferrite, depending on heat treatment. Ductile iron is stronger and more shock resistant than gray iron, so although it is more expensive due to alloyants, it may be the preferred economical choice because a lighter casting can perform the same function.

Although most versions of cast iron are often brittle, ductile cast iron has much greater fatigue and impact resistance due to its nodular graphite inclusions, which is the common defining characteristic of this group of materials. In ductile irons, graphite is in the form of nodules rather than flakes as in gray iron. Nodule formation is achieved by adding a small amount of magnesium or cerium to the alloy when in the liquid phase, the growth of graphite can be slowed during the solidification process. Whereas sharp graphite flakes create stress concentration points within the metal matrix, rounded nodules inhibit the creation of cracks, thus providing the enhanced ductility that gives the alloy its name. In fact, ductile iron has mechanical characteristics approaching those of steel, while it retains high fluidity when molten and lower melting point.
Material properties are intensive properties, that means they are independent of the amount of mass and may vary from place to place within the system at any moment. The basis of materials science involves studying the structure of materials, and relating them to their properties (mechanical, electrical etc.). Once a materials scientist knows about this structure-property correlation, they can then go on to study the relative performance of a material in a given application. The major determinants of the structure of a material and thus of its properties are its constituent chemical elements and the way in which it has been processed into its final form.
Materials are frequently chosen for various applications because they have desirable combinations of mechanical characteristics. For structural applications, material properties are crucial and engineers must take them into account.
In mechanics of materials, the strength of a material is its ability to withstand an applied load without failure or plastic deformation. Strength of materials basically considers the relationship between the external loads applied to a material and the resulting deformation or change in material dimensions. Strength of a material is its ability to withstand this applied load without failure or plastic deformation.
Ultimate tensile strength of ductile cast Iron – ASTM A536 – 60-40-18 is 414 Mpa (>60 ksi).
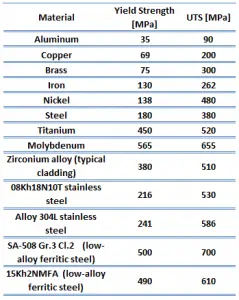
The ultimate tensile strength is the maximum on the engineering stress-strain curve. This corresponds to the maximum stress that can be sustained by a structure in tension. Ultimate tensile strength is often shortened to “tensile strength” or even to “the ultimate.” If this stress is applied and maintained, fracture will result. Often, this value is significantly more than the yield stress (as much as 50 to 60 percent more than the yield for some types of metals). When a ductile material reaches its ultimate strength, it experiences necking where the cross-sectional area reduces locally. The stress-strain curve contains no higher stress than the ultimate strength. Even though deformations can continue to increase, the stress usually decreases after the ultimate strength has been achieved. It is an intensive property; therefore its value does not depend on the size of the test specimen. However, it is dependent on other factors, such as the preparation of the specimen, the presence or otherwise of surface defects, and the temperature of the test environment and material. Ultimate tensile strengths vary from 50 MPa for an aluminum to as high as 3000 MPa for very high-strength steels.
Yield strength of ductile cast Iron – ASTM A536 – 60-40-18 is 276 Mpa (>40 ksi).
The yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning plastic behavior. Yield strength or yield stress is the material property defined as the stress at which a material begins to deform plastically whereas yield point is the point where nonlinear (elastic + plastic) deformation begins. Prior to the yield point, the material will deform elastically and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible. Some steels and other materials exhibit a behaviour termed a yield point phenomenon. Yield strengths vary from 35 MPa for a low-strength aluminum to greater than 1400 MPa for very high-strength steels.
Young’s modulus of elasticity ductile cast Iron – ASTM A536 – 60-40-18 is 170 GPa.
The Young’s modulus of elasticity is the elastic modulus for tensile and compressive stress in the linear elasticity regime of a uniaxial deformation and is usually assessed by tensile tests. Up to a limiting stress, a body will be able to recover its dimensions on removal of the load. The applied stresses cause the atoms in a crystal to move from their equilibrium position. All the atoms are displaced the same amount and still maintain their relative geometry. When the stresses are removed, all the atoms return to their original positions and no permanent deformation occurs. According to the Hooke’s law, the stress is proportional to the strain (in the elastic region), and the slope is Young’s modulus. Young’s modulus is equal to the longitudinal stress divided by the strain.
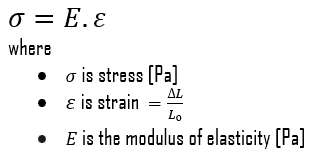
Brinell hardness of ductile cast Iron – ASTM A536 – 60-40-18 is approximately 150 – 180 MPa.
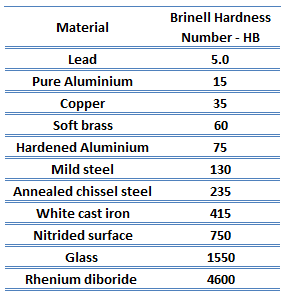
In materials science, hardness is the ability to withstand surface indentation (localized plastic deformation) and scratching. Hardness is probably the most poorly defined material property because it may indicate resistance to scratching, resistance to abrasion, resistance to indentation or even resistance to shaping or localized plastic deformation. Hardness is important from an engineering standpoint because resistance to wear by either friction or erosion by steam, oil, and water generally increases with hardness.
Brinell hardness test is one of indentation hardness tests, that has been developed for hardness testing. In Brinell tests, a hard, spherical indenter is forced under a specific load into the surface of the metal to be tested. The typical test uses a 10 mm (0.39 in) diameter hardened steel ball as an indenter with a 3,000 kgf (29.42 kN; 6,614 lbf) force. The load is maintained constant for a specified time (between 10 and 30 s). For softer materials, a smaller force is used; for harder materials, a tungsten carbide ball is substituted for the steel ball.
The test provides numerical results to quantify the hardness of a material, which is expressed by the Brinell hardness number – HB. The Brinell hardness number is designated by the most commonly used test standards (ASTM E10-14[2] and ISO 6506–1:2005) as HBW (H from hardness, B from brinell and W from the material of the indenter, tungsten (wolfram) carbide). In former standards HB or HBS were used to refer to measurements made with steel indenters.
The Brinell hardness number (HB) is the load divided by the surface area of the indentation. The diameter of the impression is measured with a microscope with a superimposed scale. The Brinell hardness number is computed from the equation:
 Brinell hardness test" width="320" height="190" />
Brinell hardness test" width="320" height="190" />
There are a variety of test methods in common use (e.g. Brinell, Knoop, Vickers and Rockwell). There are tables that are available correlating the hardness numbers from the different test methods where correlation is applicable. In all scales, a high hardness number represents a hard metal.
References: Materials Science:U.S. Department of Energy, Material Science. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
U.S. Department of Energy, Material Science. DOE Fundamentals Handbook, Volume 2 and 2. January 1993.
William D. Callister, David G. Rethwisch. Materials Science and Engineering: An Introduction 9th Edition, Wiley; 9 edition (December 4, 2013), ISBN-13: 978-1118324578.
Eberhart, Mark (2003). Why Things Break: Understanding the World by the Way It Comes Apart. Harmony. ISBN 978-1-4000-4760-4.
Gaskell, David R. (1995). Introduction to the thermodynamics of Materials (4th ed.). Taylor and Francis Publishing. ISBN 978-1-56032-992-3.
González-Viñas, W. & Mancini, H.L. (2004). An Introduction to Materials Science. Princeton University Press. ISBN 978-0-691-07097-1.
Ashby, Michael; Hugh Shercliff; David Cebon (2007). Materials: engineering, science, processing and design (1st ed.). Butterworth-Heinemann. ISBN 978-0-7506-8391-3.
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.